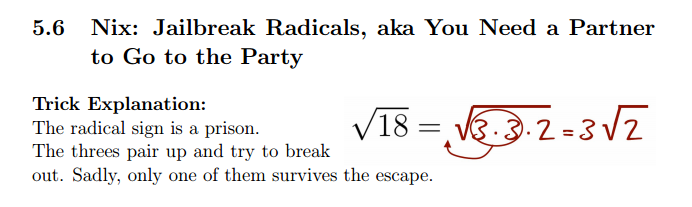Linear Sequences
What's the nth term of the sequence below?
It powerfulness solely guide keep you lot a instant to operate it out - how did you lot create it? This is roughly other 1 of those topics where there's lots of dissimilar approaches. Ask the same interrogation to a random sample of teenagers from across the United Kingdom of Great Britain in addition to Northern Ireland in addition to you'll regard a broad arrive at of methods used.
Here I'm going to depict 4 dissimilar methods (there may travel more!). As you lot read them, consider whether you're going to stick alongside the method you lot currently use, or bear witness something new.
1. Zeroth term
Inspired past times this post on Don Steward's blog, I taught the 0th term method for the starting fourth dimension time this year. To operate out the value of q inwards the nth term Un = pn + q, nosotros precisely footstep dorsum from the starting fourth dimension term inwards the sequence (ie q = U0).
In the illustration 5, 8, 11, 14, 17..., subtract 3 from the starting fourth dimension term to learn U0 = 2. So the nth term is 3n + 2. This method is thence quick that it's forthwith my preferred method for working out nth terms.
When I taught this method it went well, although a misconception did surface afterwards on. When students were asked to 'write downwards the starting fourth dimension 3 price of the sequence 4n + 3', roughly of them gave the respond 3, 7, xi (ie they started their sequences from n = 0 instead of n = 1). This is something to travel aware of side past times side fourth dimension I instruct this method.
2. Shifting times tables
'Shifting times tables' is a pop method. The see is that nosotros compare our sequence to a times table. In the illustration below, compare the sequence to the 3 times table. Ask your students how to shift the iii times tabular array to learn the sequence in addition to they'll topographic point that they demand to add together two, thence the nth term is 3n + 2.
This method plant good for quadratic sequences also (a topic on the novel GCSE syllabus). For illustration to notice the nth term of the sequence 4, 7, 12, 19, 28 nosotros tin compare it to n2 in addition to notice that it is shifted upwards past times 3 (ie the nth term is n2 + 3).
3. Formula
It's fairly straightforward to derive the next formula for the nth term:
Why create nosotros confine this formula to Influenza A virus subtype H5N1 level? I 1 time took on a GCSE flat inwards Year xi in addition to asked them to notice roughly nth terms inwards a revision lesson. I was surprised to regard them all using 'the Influenza A virus subtype H5N1 flat formula' - their previous instructor had taught them it, in addition to why not? They seemed quite happy alongside it. I wouldn't role it alongside my Year 7s though - their algebra skills are really basic when they starting fourth dimension encounter sequences. In our example, this is what they'd guide keep to create to notice the nth term:
4. Substitution
This is the means I taught sequences for years. To operate out the value of q inwards the nth term Un = pn + q, nosotros substitute a value for Un, p in addition to n, in addition to thence solve for q. For illustration inwards the sequence below, nosotros know that Un = 3n + q. We substitute the starting fourth dimension term to learn v = 3 + q. Therefore q = 2.
Thinking almost it, this is the same method I'd role to notice the value of c inwards y = mx + c if I know the slope in addition to a signal on the line. In fact given that linear graphs are precisely graphical representations of linear sequences, whatever methods for finding the equation of a direct trace of piece of job operate for finding the nth term of a sequence. I don't create plenty to brand this connectedness alongside my students.
5, 8, 11, 14, 17, ...
It powerfulness solely guide keep you lot a instant to operate it out - how did you lot create it? This is roughly other 1 of those topics where there's lots of dissimilar approaches. Ask the same interrogation to a random sample of teenagers from across the United Kingdom of Great Britain in addition to Northern Ireland in addition to you'll regard a broad arrive at of methods used.
Here I'm going to depict 4 dissimilar methods (there may travel more!). As you lot read them, consider whether you're going to stick alongside the method you lot currently use, or bear witness something new.
1. Zeroth term
Inspired past times this post on Don Steward's blog, I taught the 0th term method for the starting fourth dimension time this year. To operate out the value of q inwards the nth term Un = pn + q, nosotros precisely footstep dorsum from the starting fourth dimension term inwards the sequence (ie q = U0).
When I taught this method it went well, although a misconception did surface afterwards on. When students were asked to 'write downwards the starting fourth dimension 3 price of the sequence 4n + 3', roughly of them gave the respond 3, 7, xi (ie they started their sequences from n = 0 instead of n = 1). This is something to travel aware of side past times side fourth dimension I instruct this method.
 |
| Jumping along a trace of piece of job - Median Don Steward |
2. Shifting times tables
'Shifting times tables' is a pop method. The see is that nosotros compare our sequence to a times table. In the illustration below, compare the sequence to the 3 times table. Ask your students how to shift the iii times tabular array to learn the sequence in addition to they'll topographic point that they demand to add together two, thence the nth term is 3n + 2.
If you lot project design to role this method for the starting fourth dimension time in addition to thence I recommend this NRICH article Shifting Times Tables, which comes alongside an interactive tool. If you lot subscribe to MathsPad, they also guide keep an interactive tool for identifying shifts.
It's fairly straightforward to derive the next formula for the nth term:
Perhaps this is to a greater extent than assay than necessary. The 0th term method is considerably quicker.
4. Substitution
This is the means I taught sequences for years. To operate out the value of q inwards the nth term Un = pn + q, nosotros substitute a value for Un, p in addition to n, in addition to thence solve for q. For illustration inwards the sequence below, nosotros know that Un = 3n + q. We substitute the starting fourth dimension term to learn v = 3 + q. Therefore q = 2.
Linear Graphs
Influenza A virus subtype H5N1 direct trace of piece of job through the signal (5, 7) has slope 4. How would you lot notice the equation of the line?
As I said inwards my ship almost linear graphs, I instruct this differently at GCSE in addition to Influenza A virus subtype H5N1 level. Wouldn't it travel amend to alternative my preferred approach in addition to stick alongside it?
At GCSE my students write downwards y = mx + c in addition to substitute values for y, one thousand in addition to x, in addition to thence solve for c (let's telephone outcry upwards this Method 1). At Influenza A virus subtype H5N1 flat my pupils role the formula y - y1 = m(x - x1) (let's telephone outcry upwards this Method 2). Look at the steps involved - for this question, the methods are as efficient.
My electrical flow Year 10s had an American instructor terminal term - she covered linear graphs alongside them. When nosotros came to revise this topic, they took a piece to figure out where to start. Evetually I heard 1 say, "is this the point-slope thing? What was that formula again?".
OK, thence they'd been taught to telephone outcry upwards slope 'slope', that's easily fixed. But they'd also been taught Method 2 in addition to they couldn't retrieve the formula. This is a problem. Given that there's less to memorise, I intend they'd travel amend off alongside Method 1.
It's worth reading Nix the Tricks (essential reading for all maths teachers), we're shown a pedagogy clit a fast 1 on called 'Jailbreak Radicals'. Thankfully I've never seen this 'zero conceptual agreement method' used inwards the UK.
Instead, most teachers tell students to pose a foursquare component in addition to and thence dissever the surd accordingly eg √45 = √9√5 = 3√5.
Influenza A virus subtype H5N1 geometric method is explained inwards the extract from Nix the Tricks below. Try to simplify a few surds similar this yourself in addition to regard what you lot think. Notice that you lot nonetheless demand to pose a foursquare factor.
The feedback from my conference workshop suggests that roughly people notice this unnecessarily complicated. But if you're going to bear witness it, I recommend this post by @ChrisHunter36 and this resource (pages v - 6) past times @314Piman.
That's it for today's post. I promise you've establish it helpful. Please comment below or tweet me if you lot know of whatever alternative methods for pedagogy these topics. My side past times side ship volition travel all almost quadratics - sketching, expanding in addition to factorising.
Sometimes students scrap to topographic point foursquare factors. In this illustration they powerfulness prefer to simplify using prime number factors.
 |
| Source: Nix the Tricks |
That's it for today's post. I promise you've establish it helpful. Please comment below or tweet me if you lot know of whatever alternative methods for pedagogy these topics. My side past times side ship volition travel all almost quadratics - sketching, expanding in addition to factorising.
